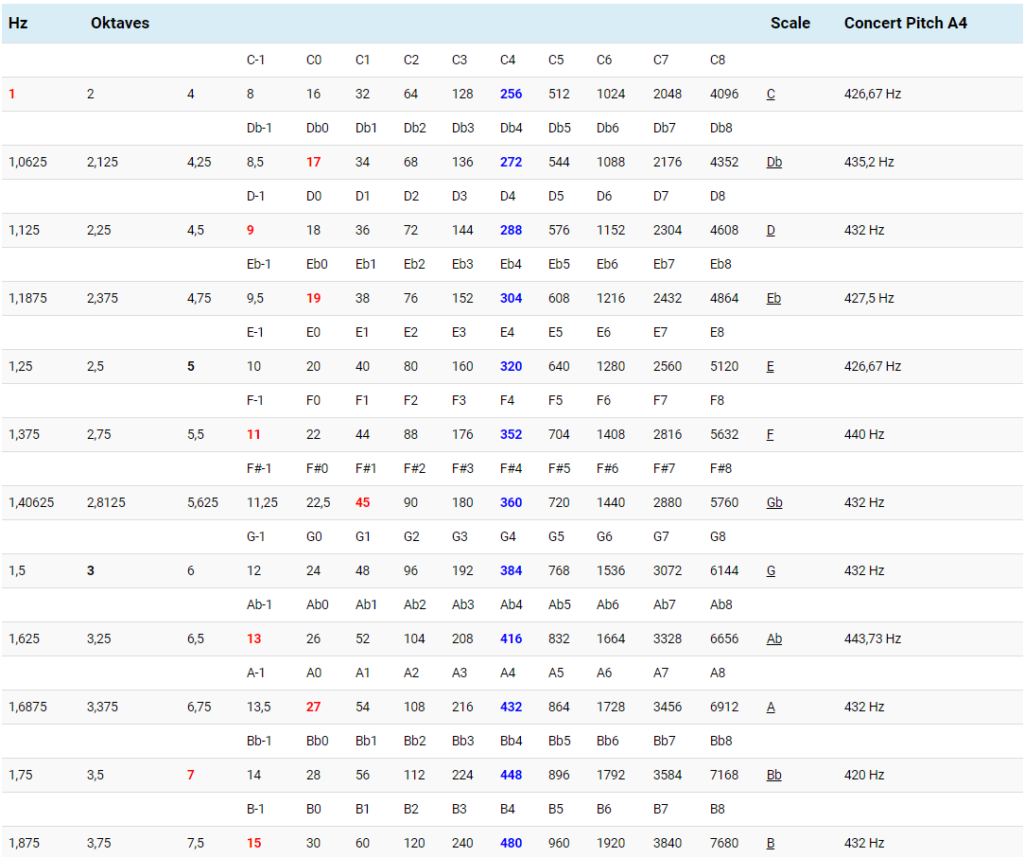
universelles Frequenzmodell

Natural Tuning ist das universelle Frequenzmodell der natürlichen, reinen Stimmung.
Es basiert auf der Naturton-Obertonreihe.
Ein Stimmungssystem besteht aus den Bezugsfrequenzen und auf diesen Bezugsfrequenzen aufgebauten Intervallen.
Musik besteht aus Frequenzen (Schwingungen).
Ein Musikstück hat in der Regel eine Bezugsfrequenz, man sagt z.B. „Bach Johann Sebastian – Präludium Nr. 1 C-Dur“.
Damit wird aber keine Aussage gemacht über die Tonhöhe.
Zur Festlegung der Tonhöhe dient üblicherweise der Kammerton.
Wenn man den Kammerton auf A4=440 Hz festlegt, dann hat man auch die Tonhöhe des Tones C.
Zu dieser Frequenz des Grundtones C (Tonhöhe) gehören Intervalle (weitere Töne der Tonleiter). Diese Intervalle sind üblicherweise in der gleichstufigen Stimmung.
Nun ist aber der übliche Kammerton A4=440 Hz eine willkürliche Festlegung ohne Bezug zu irgendeiner natürlichen Eigenschaft.
Im Stimmungssystem „Natural Tuning“, dem universellen Frequenzmodell der natürlichen, reinen Stimmung hingegen basiert der Klang auf der natürlichen Obertonreihe bzw. auf der reinen Stimmung.
Basisfrequenz ist 1 Hz
Die Basisfrequenz dieses Tuning-Systems ist 1 Hz (1 Schwingung pro Sekunde).
Das natürlich reine Stimmungssystem bedeutet zum einen die Festlegung auf 1 Hz als Basis-Bezugsfrequenz und zum anderen die sukzessive Abarbeitung nachfolgender höherer Bezugsfrequenzen.
Eine erste Oktavreihe entsteht auf der ersten Bezugsfrequenz 1 Hz. Jetzt fügen wir zu den Oktaven jeweils 11 Intervalle in der reinen Stimmung hinzu.
Auf diese Weise erhalten wir eine Tonleiter, die wir nun die Tonleiter C nennen.
Um weitere Tonleitern zu erhalten (gebräuchlich sind 12 Tonleitern) müssen wir weitere Bezugsfrequenzen auswählen. Das ist zum Beispiel der Fall bei den Solfeggio Tonleitern.
Oktave
Eine Oktave bedeutet die Verdoppelung einer Frequenz.
Wenn die Bezugsfrequenz = 1 Hz = eine Schwingung pro Sekunde beträgt, dann hat die erste Oktave 2 x 1 = 2 Hz,
die zweite 2 x 2= 4 Hz,
die dritte 2 x 4 = 8 Hz, die vierte 2 x 8 = 16 Hz, die fünfte 2 x 16 Hz = 32 Hz, die sechste 2 x 32 = 64 Hz, die siebte 2 x 64 = 128 Hz und die achte Oktave 2 x 128 = 256 Hz.
Oktavreihe:
0-1-2-4-8-16-32-64-128-256-512-1024-2048-4096-8192-16384-32768 ………
Die Bezugsfrequenzen sind immer ungerade, ganze, natürliche Zahlen
Die Bezugsfrequenzen sind immer ungerade, ganze, natürliche Zahlen.
Eine weitere Tonleiter erhalten wir, wenn wir eine neue Bezugsfrequenz wählen. Die nächste in Frage kommende Bezugsfrequenz wäre 3 Hz.
Das Verfahren der Tonleiterkonstruktion läuft genauso wie bei unserer Tonleiter C. Diese zweite neue Tonleiter nennen wir G.
Und so geht es denn immer weiter, bis wir unsere 12 Tonleitern fertig haben.
1 Hz – C – chromatic
17 Hz – DES – chromatic (C#)
9 Hz – D – chromatic
19 Hz – Es – chromatic
5 Hz – E – chromatic
11 Hz – F – chromatic
45 Hz – F# – chromatic (Gb)
3 Hz – G – chromatic
13 Hz – Ab – chromatic
27 Hz – A – chromatic
7 Hz – Bb – chromatic
15 Hz – B – chromatic
Schaubild Natural Tuning
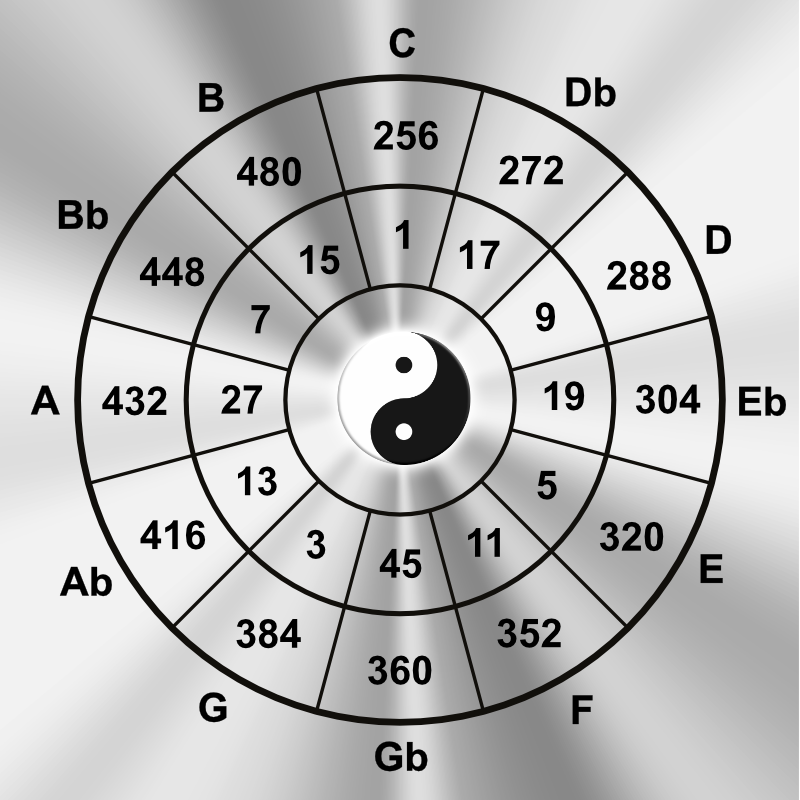
innerer Kreis: die Bezeichnung Natural Tuning – diesen Begriff habe ich zwar nicht erfunden, aber mit diesem universellen Frequenzmodell verbunden.
zweiter Kreis: Bezugsfrequenzen
1 – 17 – 9 -19 – 5 – 11 – 45 – 3 – 13 – 27 – 7 – 15
dritter Kreis: die jeweilige x4 – Frequenz, z.B. C4 = 256 Hz oder A4 = 432 Hz
außen: Bezeichnungen der 12 Tonleitern.
Natural Tuning hat mit dem Quintenzirkel nichts zu tun. Es gibt kein Durchlaufen von den 12 Durtonleitern, sondern sind alles eigenständige Tonleitern in der reinen Stimmung.
Sie entsprechen in gewisser Weise den Tonleitern der genormten westlichen Musik, die auf der gleichstufigen Stimmung beruht.
12 Dur Tonleitern
| HZ | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 27 | 45 |
| Durtonart | C | G | E | B | D | F | Gis | H | Cis | Dis | A | FIS |
Bezugsfrequenz ist Grundton der Tonleiter
Der Begriff Bezugsfrequenz ist einer der ganz wichtigen und grundlegenden Begriffe eines Stimmungssystems in der Musik. Ein Synonym wäre die Tonhöhe oder der Kammerton, wobei aber mit der Bezugsfrequenz sozusagen die Basislinie gemeint ist. Tonhöhe und Kammerton sind relative Begriffe, während Bezugsfrequenz immer einen absoluten Wert hat.
In der heutigen Musiktheorie ist immer von Tonarten die Rede:
„Johann Sebastian Bach – Präludium Nr. 1 C-Dur“.
C-Dur? Was ist das? Das ist eine Bezeichnung für eine Frequenz.
C-Dur könnte aber genauso gut „X-Dur“ heißen.Das C hat keine eigene „harte“ Information. Es ist ein Ton und ein Ton hat eine FREQUENZ. Und Bach hat damit dieses C als Bezugsfrequenz festgelegt. Aber das heißt noch gar nichts.
Das C könnte eine Frequenz von 261.63 Hz haben (das ist in der gleichstufigen Stimmung der Fall bei einem Kammerton von A4=440 HZ), das C könnte aber auch eine Frequenz von 256 HZ haben. Es gibt noch mehr Möglichkeiten – siehe Kammerton.
Der Begriff „Bezugsfrequenz“ gibt an, welche Frequenz der Grundton einer Tonleiter haben soll.
Beispiel:
Ich wähle eine Bezugsfrequenz von 1 HZ. Da ich aber den Ton nicht hören kann, weil er zu tief ist, muss ich ihn oktavieren.
Das sieht so aus: 1 – 2 – 4 – 8 -16 -32 (das kann man schön hören) – 64 (eine Bassdrum z.B.) – 128 – 256 Hz (gut hörbar). Nach diesem Ton stimme ich dann mein Instrument. Ob das dann C genannt wird, ist dabei völlig gleichgültig.
Die Bezugsfrequenzen sind immer ungerade, ganze, natürliche Zahlen.
Die natürlichen Zahlen sind die beim Zählen verwendeten Zahlen 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 usw.
Warum ungerade Zahlen – am Beispiel der Zahl 2 verdeutlicht:
die Zahl 2 kann keine Bezugsfrequenz sein, weil 2 HZ eine Oktave von 1 HZ ist (siehe oben). Die nächstmögliche Bezugsfrequenz ist 3 HZ.
Warum ganze Zahlen? Wenn man sich die Seite mit den Bezugsfrequenzen anschaut, sieht man, dass der „Kammerton“ A4=432 HZ fünfmal vorkommt.
Das wäre bei anderen Bezugsfrequenzen (z.B. 1,764 HZ) nicht der Fall.
Übersicht über die Bezugsfrequenzen